Inferring utility functions from locally non-transitive preferences
TL;DR: Fanboying JvN, then a nuts-and-bolts description of the von-Neumann-Morgenstern theorem. A connection to reward modeling, some simulations, and pretty figures!
Johnny did it.
Last week I offhandedly mentioned the unlikely possibility that my coworkers are clones of John von Neumann. I need to explain that a bit more ——— It was a compliment, I swear! John von Neumann was... a "genius" doesn't quite do it justice. The "Last Great Polymath"? The "Man from the Future"? The "life of the party," "an occasional heavy drinker," and "reckless driver"1? Okay, that last one again isn't very flattering. I'm trying to say that von Neumann was an interesting person who did many interesting things.

Remember when I claimed that Claude Shannon came up with the minimax decision rule? I was wrong; Johnny did it 20 years earlier. The architecture of modern computers? Johnny did it. A mathematical foundation of utilitarian ethics? Johnny did... what?
Well, it's a bit complicated. Here’s my reasoning:
Preference utilitarianism and the Von-Neumann-Morgenstern theorem. Ethics is the part of philosophy concerned with the question, "How should I act?" One possible answer to that question is utilitarianism, prescribing that we should maximize happiness and well-being for all affected individuals. Achieving "happiness and well-being" is undoubtedly desirable (or?), but kind of hard to operationalize. Instead of asking people about what they want, we might also observe what people prefer when given a choice. Preference utilitarianism is a form of utilitarianism that focuses on satisfying everyone's preferences. And it turns out that, if you are being reasonable about your preferences, we can represent your preferences succinctly in a "utility function," u(A). This utility function has the neat property that for two possible options, L and M, you prefer option M over option L iff2 u(M) > u(L).
This is one way to arrive at the "von-Neumann-Morgenstern theorem," but it's probably not the path von Neumann took when deriving it3.
But I think it’s an interesting perspective. There is a seemingly straightforward way to use the theorem to solve some nasty technical problems related to “making machines try to do what humans want them to do.” Get everyone's utility functions, combine them, and then pick the actions that increase them the most. While you and I probably can't do that, perhaps a computer can help - they are very good at making numbers go up! And perhaps there is a case to be made that utility is effectively the best single number we can hope for.
Sounds good. Where is the catch?
The futility of computing utility.
Let's start by trying to write down a utility function. The proof of the von-Neumann-Morgenstern is constructive, i.e., it doesn't only guarantee the existence of a utility function, it also shows us the way to get there. Here is a step-by-step guide:
1. Write down all the possible elementary outcomes that we might want to know the utility of.
Ah. Yeah. That's going to be a problem.
"All the things" is a lot of things. We might (and will, in this post) limit ourselves to a toy domain to make some progress, but that will be a poor substitute for the thing we want: all the possible outcomes affecting all existing humans. We might not even think of some outcomes because they appear too good to be true. (Or too weird to be thinkable.) We might even want to include those outcomes in particular, as they might be the best option that nobody realized was on the table. But if we can't think of them, we can't write them down.
(Perhaps there is a way out. An essential nuance in the first step is writing down "all the possible elementary outcomes." We don't need to consider all the outcomes immediately. We only need to consider a set from which we can construct the more complicated outcomes. We need a basis of the space of possibilities. That's already infinitely easier, and we're always guaranteed to find a basis (if we're willing to embrace chaos). The hope here might now be that we can find a basis of a system that is rich enough to describe all relevant outcomes and simple enough to allow for linear interpolation. Of course, a semantic embedding of natural language comes to mind, but the imprecision of language is probably a deal-breaker. Perhaps the semantic embedding of a formal language/programming language is more appropriate4?)
Let's use a toy domain, call this an open problem, and move on.
2. Order all the elementary outcomes from worst to best.
For some inexplicable reason, my intro to computer science course at uni has prepared me for this exact task, and this task alone. We have a bunch of great algorithms for sorting the elements of a list by comparing them with each other. If we're not incredibly unlucky, we can hope to sort N-many outcomes with
comparisons. After sorting thousands of elementary outcomes, we pick the worst (bumping your toe against a chair5) and the best (ice cream sandwich) and assign them utility 0 and 1. For 1000 elementary outcomes, we could do with as little as 3000 comparisons which you could knock out in an afternoon. For 100000 elementary outcomes, we're talking 500000 comparisons which will keep you busy for a while. But it's for a good cause!
Unless... somebody screws up. Those 3000 comparisons have to be spot on. If you accidentally mess up one comparison, the sorting algorithm might not be able to recover6. And since we're working with humans, some errors are guaranteed. Can you confidently say that you prefer a mushroom risotto over a new pair of shoes? Thought so.

But now comes the real killer.
3. Do a sequence of psychophysics experiments where humans indicate where the exact probabilistic combination of the worst- and the best possible outcome is equivalent to an intermediate outcome.
After sorting all outcomes from worst to best, we offer you a sequence of lotteries for each intermediate outcome (mushroom risotto): "Would you rather accept a 10% chance of stubbing your toe and a 90% chance of an ice cream sandwich, or a guaranteed mushroom risotto?" At some point (45% stubbing your toe), your answer will change from "Yes" to "No," and then we know we are very close to finding your utility for mushroom risotto (in this case, a utility of ~0.45).
I was halfway through setting up MTurk, but let's be realistic - this will not work. Allais paradox aside, I don't have the patience to set this up, so who will have the patience to go through this? Of course, we should have seen this coming. Just because a proof is "constructive" doesn't mean that we can apply it in the messy real world. Getting a utility function out of a human will require some elbow grease.
Human fallibility and reward modeling.
Let’s shuffle some symbols. How do we account for all the human messiness and the tendency to make mistakes? A standard trick is to call it "noise"7. Given a true estimate of utility, ū(A), we might write the perceived utility at any given time as a random variable, u(A), distributed around the true value,
Given two outcomes, O₁ and O₂, the probability of assessing the utility of O₂ higher than the utility of O₁ is distributed as the difference of two Gaussians, which is again a Gaussian:
(assuming independence of O₂ and O₁). The error function (lovingly called erf) is nasty because it doesn't have a closed-form solution. But it does have a close relative that looks almost the same and is a lot nicer mathematically, and that has a much more pleasant-sounding name than "erf"...
I'll replace the erf with a stereotypical logistic function, S,
Much nicer. Even though the logistic function has largely fallen out of favor as an activation function in machine learning, its grip on psychophysics is unbroken.
Now that we have the mathematical machinery in place, we need to calibrate it to reality. A natural choice is to take the cross-entropy between our machinery, P(u(O₂) > u(O₁)), and the actual comparisons provided by humans, (O₂ > O₁) or (O₁ > O₂),
Surprise8! The resulting loss function is also used for the reward modeling that I briefly touched on in last week's post9. The researchers who originally proposed this technique for learning human preferences say that it is similar to the Elo rating system from chess and the "Bradley & Terry model." I find the motivation of reward modeling as an approximation of the von-Neumann-Morgenstern theorem a lot more Romantic, though.
Having uncovered this connection, a natural strategy for inferring a utility function through training a neural network with comparisons of pairs of elements from the domain presents itself.

Can this work? It doesn’t involve MTurk for now, so I am happy to try!
A natural representation of utility functions.
I found that the neural network achieves near-zero loss on the comparisons after 20k steps (panel a). Runtime appears to increase linearly with the number of elements10. The resulting utility functions are monotonic and increase by an (approximately) equal amount from one item to another (panel b). This demonstrates that given enough time, a multilayer perceptron can sort a list.

Some might say that I used several hours of compute time on a Google Colab GPU just to sort lists, but that would be rather uncharitable. My primary motivation for this approach (human tendency to make mistakes) bears fruits in the following experiment. When I add noise to the choice procedure (resulting in 10% “random” choices), the network is still able to recover the appropriate ordering (panel c). And, even more remarkable, when I make the choice procedure loopy (i.e., nontransitive), the network can still recover a reasonable approximation of what the utility function looks like (panel d)!
This last set of experiments is exciting because introducing loops leads to nonlinear utility functions that are squashed together in the vicinity of the loop. Intuitively, if outcomes #3 and #4 are impossible to distinguish reliably, this might indicate that their utility is indeed very similar. The exciting possibility is that step 3 of the procedure above (psychometric calibration of utilities) could automatically be satisfied when options are sufficiently similar and sometimes confused11.
Concluding thoughts and what’s next?
There are a lot more experiments I want to run on this toy domain to probe the limits to which preference orderings can be turned into utility functions:
What is the largest number of elements we can sort with a given architecture? How does training time change as a function of the number of elements?
How does the network architecture affect the resulting utility function? How do the maximum and minimum of the unnormalized utility function change?
Which portion of possible comparisons needs to be presented (on average) to infer the utility function?
But independent of those experiments, there are some fascinating directions that I plan to explore in a future post. Now that I have a natural way to induce utility functions, I think I can further explore the utility monster and some of the classic literature on (un-)comparability of utility functions. I also really want to write a proper treatment of value handshakes, which is a topic in dire need of exploration.
To stay up to date for when I write those, consider signing up for the newsletter. It’s free (and will stay free)!
What is it with intelligent people and self-medication? Also, He loved to eat, especially rich sauces and desserts, and in later years was forced to diet rigidly. To him exercise was “nonsense.” A good reminder not to fall for the Halo effect.
If and only if.
Has anybody ever looked at that? What happens when I subtract Fizzbuzz from the Fibonacci sequence?
A very close "win" over S-risk scenarios.
And the worst-case runtime shoots up to ∞ as soon as you have the probability of errors). In this situation, Bogosort might just be the most reliable solution - at least it won't terminate until it's done.
Joke aside, it’s an interesting question which factors need to come together to make something “noise.” I guess the central limit theorem can help if there are many independent factors, but that’s never really the case. The more general question is under which circumstances the residual factors are random and when they are adversarial.
Please ignore that it's already written in the section title.
The original Leike paper has an equivalent expression that does not write out the logarithm applied to the sigmoid.
My money would be on O(n log n) or worse, of course.
I’d expect that the difference in utility, |ū(O₁) - ū(O₂)|, will be proportional to the probability of confusing the order, P(u(O₁) > u(O₂)).






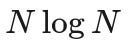



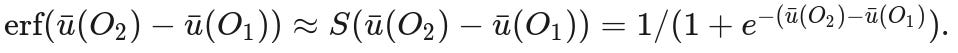


I'm not sure I understand what the neural net stuff at the end is about. If you are doing noisy sorting, that doesn't require neural networks, and there are lots of known algorithms: https://gwern.net/Resorter#noisy-sorting (You are right that noisy comparison sorting turns out to be much the same, complexity wise, as noise-free comparison sorting.) You can also make sorting and ranking directly differentiable (https://gwern.net/GPT-2-preference-learning#grover-et-al-2019), which would probably be much more efficient than trying to brute force it by iterating a MLP (wouldn't that approach bloat any NN you tried to do that inside of as a component? You'd have to unroll it for a small fixed number of iterations, I guess, and weight-tie it).